Краткое изложение истории появления и развития понятия «аликвотные дроби»
Как мы знаем из курса всеобщей истории, ещё с древних времён, люди, чтобы не умереть от голода охотились, но делали это вместе. После охоты они делили между собой пищу. С этого момента они начали задумываться о значении дробей.
Древние египтяне пользовались такими дробями, в числителе которых стоит единица. Сейчас такие дроби в математике называются аликвотными.
аликвотных дробей с разным числом слагаемых
Примеры аликвотных дробей:
1) 15/24=3+12/24=3/24+12/24=18+1/2
2) 5/13=5/13×3/3=15/39=13/39+2/39=1/3+1/20+1/780
2/39=2/39×20/20=40/780=39+1/780=39/780 +1/780=1/20+1/780
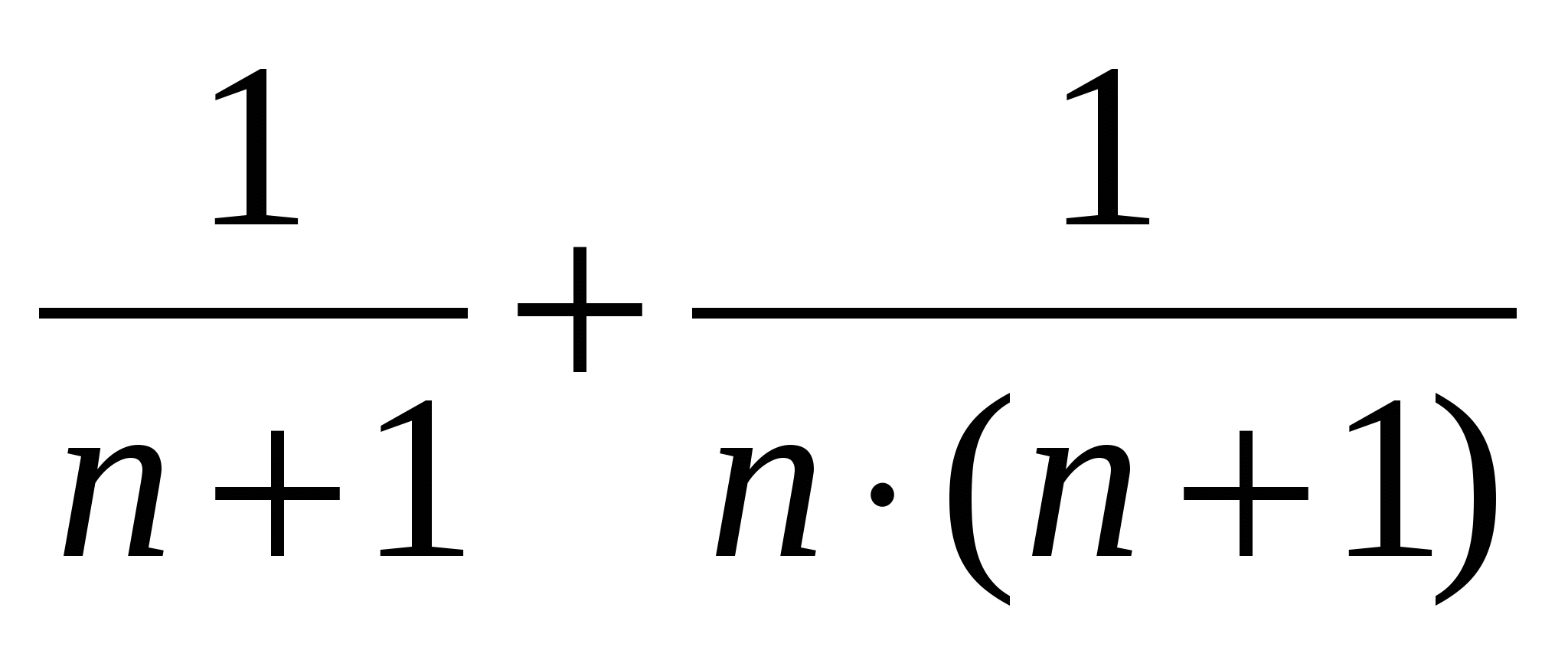
Объяснение используемого выше алгоритма.
Чтобы дробь с составным знаменателем превратить в аликвотную дробь, нужно разложить дробь на сумму двух дробей, у которых при сокращении числителя и знаменателя, в числители будет единица. В случае с дробью с простым числом в знаменателе,всë намного сложнее. Для того чтобы разложить такую дробь нужно подобрать наименьший дополнительный множитель, после которого числитель будет больше первоначального знаменателя. Далее раскладываем на сумму двух дробей, у которых при сокращении в числители будет единица и т. д.
Существующие научные гипотезы о возникновении шестидесятеричной системы счисления.
Возникновение шестидесятеричной системы не совсем понятно.
Существует несколько гипотез. Одна из них-это гипотеза И. Н. Веселовского. Она связана с счётом на пальцах. Также есть гипотеза О. Нейгебауэра. Он предполагал, что после взятия шумерского государства в нëм одновременно существовали две денежные единицы: мина и шекель(сикль).Они соотносились так: 1 мина = 60 шекелей.
Чуть позже это деление стало привычным для всех .
Авторская обоснованная оценка наиболее правдоподобной гипотезы.
Мы считаем, что гипотеза О. Нейгебауэра правдоподобнее гипотезы И. Н. Веселовского, т. к. теорию Веселовского люди критиковали, а гипотезу Нейгебауэра считали более точной и верной.
Информация о назначении клинописных математических вавилонских таблиц.
Учëные нашего времени до сих пор находят на территории древнего Вавилона клинописные математические таблички. Расшифровывая эти таблички, они не раз сталкивались с упоминанием процентов. Сохранились названия арифметических действий того времени. Сложение называлось "прибавление" или "накопление ". Умножение выражало глагол "скушать", а вычитание обозначалось словом "вырывать". Тексты на табличках свидетельствуют о том, что вавилонские математики умели выполнять более сложные алгебраические и геометрические действия.
Например: решать специальные задачи, которые включают до десяти уравнений с десятью неизвестными; отдельные разновидности кубических уравнений и уравнений четвëртой степени. Квадратные уравнения использовали при измерении площадей и объемов.
При решении уравнений с двумя неизвестными, одно называлось "шириной" , а другое "длиной ".
Их произведение называли "площадью". Прямо как и
сейчас! В кубических уравнениях существовала третья неизвестная величина - "глубина" , а их произведение называлось "объëмом ". Можно сделать вывод, что значение клинописных табличек напрямую отразилось в нашем мире.
Происхождение римской системы дробей
Римская система дробей была связана с мерой веса. Она называлась "асс". Делилась на 12 долей:
1/12 - унция
1/2 - семис
1/6 - секстанс
1/24 - семиунция
1/3 - триенс
1/228 - скрупулус
Но такая система была не совсем удобная.
Невозможно было представить число в виде дроби с знаменателем 100 или 10.
Тогда римские математики начали использовать проценты.
Примеры из современной устной речи, связанные с римской системой дробей
В настоящее время люди тоже используют римскую систему дробей в устной речи. Например мужчина придя в строительный магазин, может использовать фразу
" Я хочу купить унцию от этой фанеры. "
Страна, в которой до сих пор пользуются в системе мер и в денежной системе остатками римской системы дробей
Вес унции = 28,35 грамма. Сейчас проходя по улице в Нидерландах можно услышать слово унция. В данном случае речь идёт о 100 граммах. Это понятие также используют в Алжире, Тунисе, Египте. Но там унция, это более 30 граммов.В каждой стране унция имеет разное количество граммов.
Авторские обоснованные рассуждения о том, какая система дробей Древнего мира являлась наиболее развитой
Мы думаем, что в древнем Вавилоне была более развитая система дробей. Потому, что их система имела больше возможностей, нежели другие. Ведь вавилонские математики решали очень сложные задачи с помощью этой системы. Они решали уравнения с десятью неизвестными, решали квадратные уравнения, что для того времени было на уровне невозможного. И наверно благодаря математике Вавилон расцвел и стал культурным центром мира.
